Fiat currencies
Crypto Currencies
No results for ""
We couldn't find anything matching your search.Try again with a different term.
The Time Value of Money: How to Calculate It and How to Use It
The time value of money (TVM) is a financial concept that explains why a dollar today is worth more than a dollar in the future. It is based on the idea that money can grow over time by earning interest or being invested. Therefore, receiving money sooner rather than later allows one to exploit its potential growth.
In this article, we will explore the following topics:
- What are the factors that affect the time value of money?
- How to calculate the present and future value of money using formulas and examples?
- What are the applications and implications of the time value of money in personal and business finance?
- How does the time value of money apply to Crypto?
Factors That Affect the Time Value of Money
There are three main factors that influence the time value of money: interest rate, compounding frequency, and inflation.
Interest Rate
The interest rate is the percentage of money paid or earned per period (such as a year, a month, or a day) for borrowing or lending money. The higher the interest rate, the more money one can earn or pay over time. Therefore, the interest rate reflects the opportunity cost of holding or spending money now versus later.
For example, if you have $1,000 today and you can invest it at a 10% annual interest rate, you will have $1,100 after one year. However, if you spend that $1,000 today, you will miss out on the $100 that you could have earned by investing it. Hence, the interest rate measures how much more money you can have in the future by saving or investing your money today.
Compounding Frequency
The compounding frequency is the number of times per year that interest is added to the principal amount of money. The more frequently interest is compounded, the faster money grows over time. Therefore, the compounding frequency reflects the earning potential of money over time.
For example, if you have $1,000 today and you can invest it at a 10% annual interest rate compounded annually, you will have $1,100 after one year. However, if you invest it at the same interest rate compounded monthly, you will have $1,104.71 after one year. Hence, the compounding frequency affects how much money you can have in the future by saving or investing your money today.
Inflation
Inflation is the general increase in the prices of goods and services over time. The higher the inflation rate, the less purchasing power money has over time. Therefore, inflation reflects the erosion of value of money over time.
For example, if you have $1,000 today and you can buy 100 units of a good that costs $10 each, you will have a purchasing power of 100 units. However, if the price of that good increases by 5% per year due to inflation, you will only be able to buy 95.24 units after one year with the same amount of money. Hence, inflation affects how much goods and services you can buy in the future with your money today.
How to Calculate the Present and Future Value of Money?
The present value (PV) of money is the amount of money that a future sum of money is worth today. The future value (FV) of money is the amount of money that a present sum of money will be worth in the future. To calculate the present and future value of money, we need to use formulas that take into account the interest rate, compounding frequency, and number of periods.
Present Value Formula
The present value formula is:
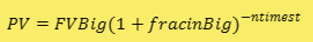
where:
- PV = Present value of money
- FV = Future value of money
- i = Interest rate per period
- n = Number of compounding periods per year
- t = Number of years
The present value formula tells us how much we need to invest today to get a certain amount of money in the future. It also tells us how much we are willing to pay today for a future stream of income or cash flow.
For example, if we want to have $10,000 in 5 years and we can invest our money at a 6% annual interest rate compounded monthly, we can use the present value formula to find out how much we need to invest today:

This means that we need to invest $7,417.25 today to get $10,000 in 5 years at a 6% annual interest rate compounded monthly.
Alternatively, if we are offered to receive $10,000 in 5 years and we want to know how much we are willing to pay for it today, we can use the same formula to find out the present value of that future payment:

This means that we are willing to pay $7,417.25 today for a future payment of $10,000 in 5 years at a 6% annual interest rate compounded monthly.
Future Value Formula
The future value formula is:
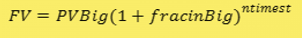
where:
- FV = Future value of money
- PV = Present value of money
- i = Interest rate per period
- n = Number of compounding periods per year
- t = Number of years
The future value formula tells us how much money we will have in the future if we invest a certain amount of money today. It also tells us how much a present stream of income or cash flow will be worth in the future.
For example, if we invest $5,000 today and we can earn an 8% annual interest rate compounded quarterly, we can use the future value formula to find out how much money we will have in 10 years:

This means that we will have $10,863.29 in 10 years if we invest $5,000 today at an 8% annual interest rate compounded quarterly.
Alternatively, if we receive $500 every quarter for 10 years and we want to know how much that stream of income will be worth in the future, we can use the same formula to find out the future value of that annuity:

This means that the stream of income of $500 every quarter for 10 years will be worth $9,306.97 in the future at an 8% annual interest rate compounded quarterly.
Applications and Implications of the Time Value of Money
The time value of money is an important concept in personal and business finance. It helps us make better decisions about saving, investing, borrowing, and spending money. Here are some examples of how the time value of money can be applied and what implications it has for different situations:
Saving and Investing Money
The time value of money shows us that saving and investing money today can help us achieve our financial goals in the future. By taking advantage of the power of compounding interest, we can grow our money faster and reach our desired future value sooner.
For example, if we want to save $100,000 for retirement in 20 years and we can invest our money at a 7% annual interest rate compounded annually, we can use the present value formula to find out how much we need to save every year:

This means that we need to save $25,841.92 every year for 20 years to have $100,000 for retirement at a 7% annual interest rate compounded annually.
However, if we start saving earlier and have more time to invest our money, we can reduce the amount that we need to save every year. For example, if we start saving 30 years before retirement instead of 20 years, we can use the same formula to find out how much we need to save every year:

This means that we only need to save $13,135.45 every year for 30 years to have $100,000 for retirement at a 7% annual interest rate compounded annually.
Hence, the time value of money shows us that saving and investing early can help us save more money in the long run.
Borrowing and Spending Money
The time value of money also shows us that borrowing and spending money today can cost us more money in the future. By paying interest on loans or credit cards, we reduce our future wealth and limit our financial options.
For example, if we borrow $10,000 today and we have to pay it back in 5 years with a 12% annual interest rate compounded monthly, we can use the future value formula to find out how much we will have to pay back in total:

This means that we will have to pay back $17,623.42 in 5 years if we borrow $10,000 today at a 12% annual interest rate compounded monthly.
However, if we pay off our debt sooner and reduce the time that we have to pay interest, we can save money in the long run. For example, if we pay off our debt in 3 years instead of 5 years, we can use the same formula to find out how much we will have to pay back in total:

This means that we will only have to pay back $14,052.85 in 3 years if we borrow $10,000 today at a 12% annual interest rate compounded monthly.
Hence, the time value of money shows us that borrowing and spending wisely can help us avoid unnecessary interest payments and debt.
How does Crypto Compare to Traditional Assets in Terms of TVM?
Traditional assets, such as stocks, bonds, and real estate, have well-established methods of valuing them based on their expected future cash flows, dividends, rents, or earnings. These methods use TVM to discount the future values of these assets to their present values, taking into account factors such as interest rate, inflation, risk, and growth.
For example, if you want to buy a bond that pays $100 every year for 10 years and has a face value of $1,000 at maturity, you can use TVM to calculate how much you are willing to pay for it today. Assuming an interest rate of 5%, you can use the present value formula to find out the present value of the bond:
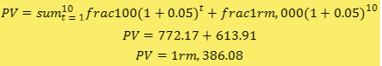
This means that you are willing to pay $1,386.08 today for a bond that will pay you $2,000 in total over 10 years at a 5% interest rate.
However, crypto assets, such as Bitcoin, Ethereum, and other altcoins, do not have any inherent cash flows, dividends, rents, or earnings. They are purely driven by supply and demand in the market, which are influenced by various factors such as technology, innovation, adoption, regulation, sentiment, speculation, and hype.
Therefore, valuing crypto assets based on TVM is not straightforward or reliable. There is no consensus on what is the appropriate discount rate or growth rate to use for crypto assets. Moreover, crypto assets are highly volatile and unpredictable, making it difficult to estimate their future values with any degree of confidence.
For example, if you want to buy Bitcoin today and expect it to be worth $100,000 in 10 years, you can use TVM to calculate how much you are willing to pay for it today. Assuming a discount rate of 10%, you can use the present value formula to find out the present value of Bitcoin:

This means that you are willing to pay $38,554.87 today for a Bitcoin that will be worth $100,000 in 10 years at a 10% discount rate.
However, this valuation is based on many assumptions and uncertainties. What if Bitcoin crashes tomorrow or never reaches $100,000? What if the discount rate changes over time or differs from person to person? What if there are new technologies or regulations that affect the demand or supply of Bitcoin? These questions make it hard to apply TVM to crypto with any accuracy or consistency.
How Can Crypto Investors Use TVM to Make Better Decisions?
Despite the challenges and limitations of applying TVM to crypto, it is still a useful concept for crypto investors to understand and use. TVM can help crypto investors make better decisions by:
- Comparing different crypto assets based on their potential returns and risks
- Evaluating different investment strategies based on their time horizons and opportunity costs
- Assessing different scenarios based on their probabilities and outcomes
Conclusion
The time value of money is a fundamental concept in finance that helps us understand the relationship between money and time. It tells us that money has different values at different points in time due to factors such as interest rate, compounding frequency, and inflation. By using formulas to calculate the present and future value of money, we can make better decisions about saving, investing, borrowing, and spending money. The time value of money can help us achieve our financial goals and optimize our financial well-being.
Stay tuned to CoinCarp Social Media and Discuss with Us:
Up to $6,045 Bonuses
Sponsored
Join Bybit and receive up to $6,045 in Bonuses! Register Now!
- Recover Lost Crypto: Fixing Wallet Issues, Seed Phrase Problems, and More Beginner 5m
- Essential Tools for AI Enthusiasts to Manage Their Crypto Beginner 8m
- NOW Wallet Review: Securely Store AI Coins Like FET & GRT Beginner 5m
- What Is the Global Dollar Network (USDG) and How Does It Work? Beginner 4m